\( G_{H^+} + G_{e^-} = -\frac{1}{2} G_{H_2} \)
The free energy of the proton is potential-independent and the potential dependence of the electron is given by the potential with respect to the standard hydrogen electrode (SHE).
\( G_{e^-} = G_{e^-}^0 - U_{SHE}\)
This then allows one to estimate the Limiting Potential \(U_{L}\) at which an electrochemical step becomes favorable by dividing the free energy change of that step by the number of electrons transferred
\( U_{L} = -\frac{\Delta G_{step}}{N_{e}} \)
This approach has been widely successful in predicting electrocatalyst activity across a variety of reactions. [1] [2] [3]
However, the CHE model cannot handle non proton-coupled electron transfer steps and enforces an integer number of electrons transferred in each step. For many reactions, there is significant evidence of fractional electron transfers as well as electron transfers that do not involve proton transfers. [4] To capture these phenomena, it is necessary to simulate the system at fixed electron potential and allow the number of electrons to self-consistently vary. I perform these simulations using Grand Canonical DFT (GC-DFT), which allows me to study systems under true fixed potentials.
Using GC-DFT takes away the easy interpretability of \(U_{L}\) and requires a different catalyst activity descriptor that has no formal potential dependence. I developed \( \Phi_{max} \), a thermodynamic approximation of the energetic span, which measures the largest barrier in a cyclic catalytic cycle. I used this descriptor to re-evaluate the typical CHE volcano plots for the electrochemical nitrogen reduction reaction to understand how explicit inclusion of potential changes catalyst scaling relations. [5]
Furthermore, we found that traditional electronic structure descriptors like d-band and p-band centers were unable to predict trends in binding energy across the dataset. We believe this is due to the highly geometry-dependent change in the renormalized adsorbate frontier orbital energies, which lead to substantially different degrees of bonding for materials with similar d-band centers. To correctly precict trends in binding energy across complex material spaces, it is necessary to incorporate the geometry of the surface.
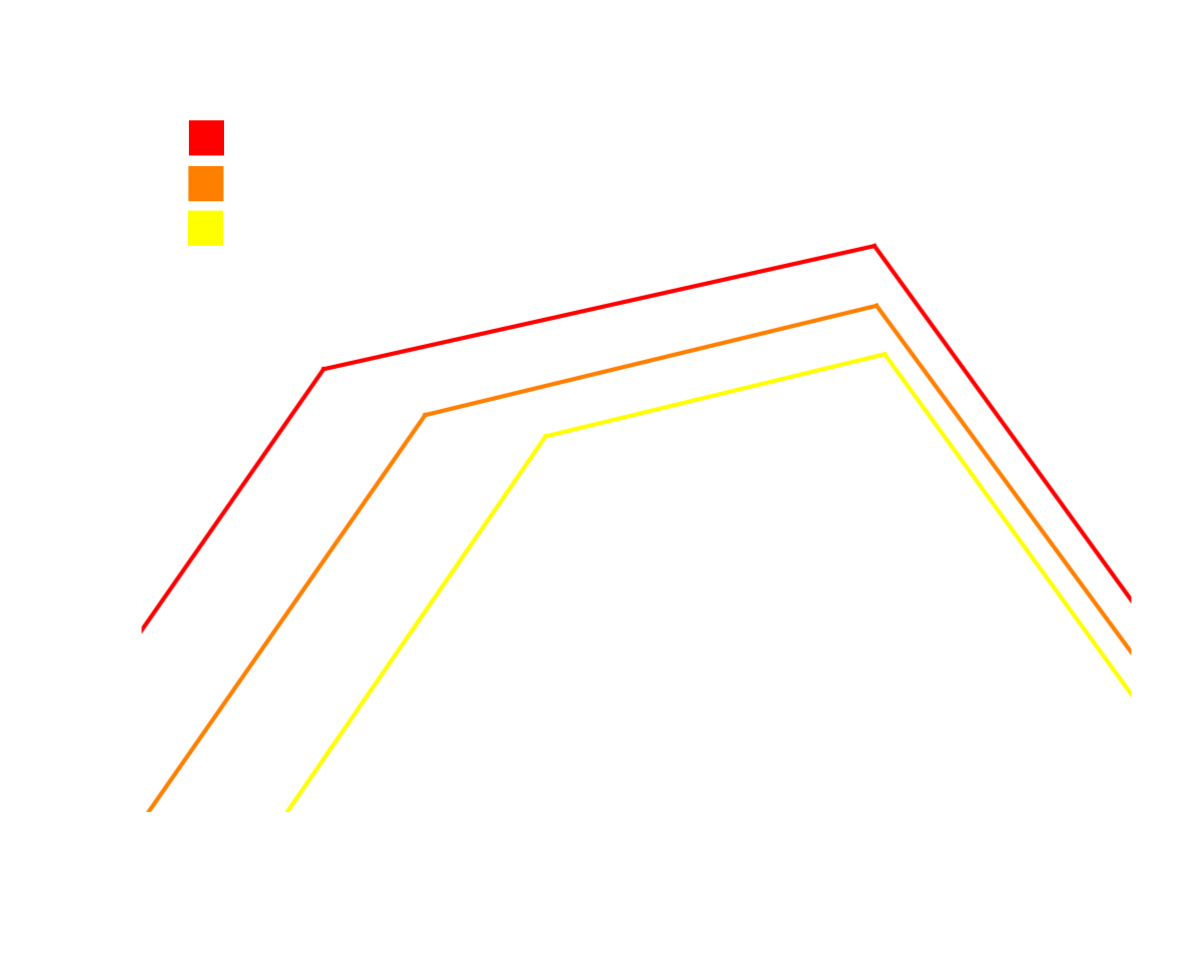
Re-evaluated nitrogen reduction reaction scaling relations using GC-DFT and the \( \Phi_{max} \) activity descriptor. Unlike
previous scaling relations, there is a flat peak shaving off the top of the volcano due to the chemical desoption of \( NH_3 \) that is less sensitive
to the applied potential than the left and right scaling lines, which are comprised of explicit electron transfer steps. These volcanos indicate that
tuning the activity of catalysts near the peak of the volcano at modest potentials necessitates selective destabilization of the \( NH_3^* \) state.
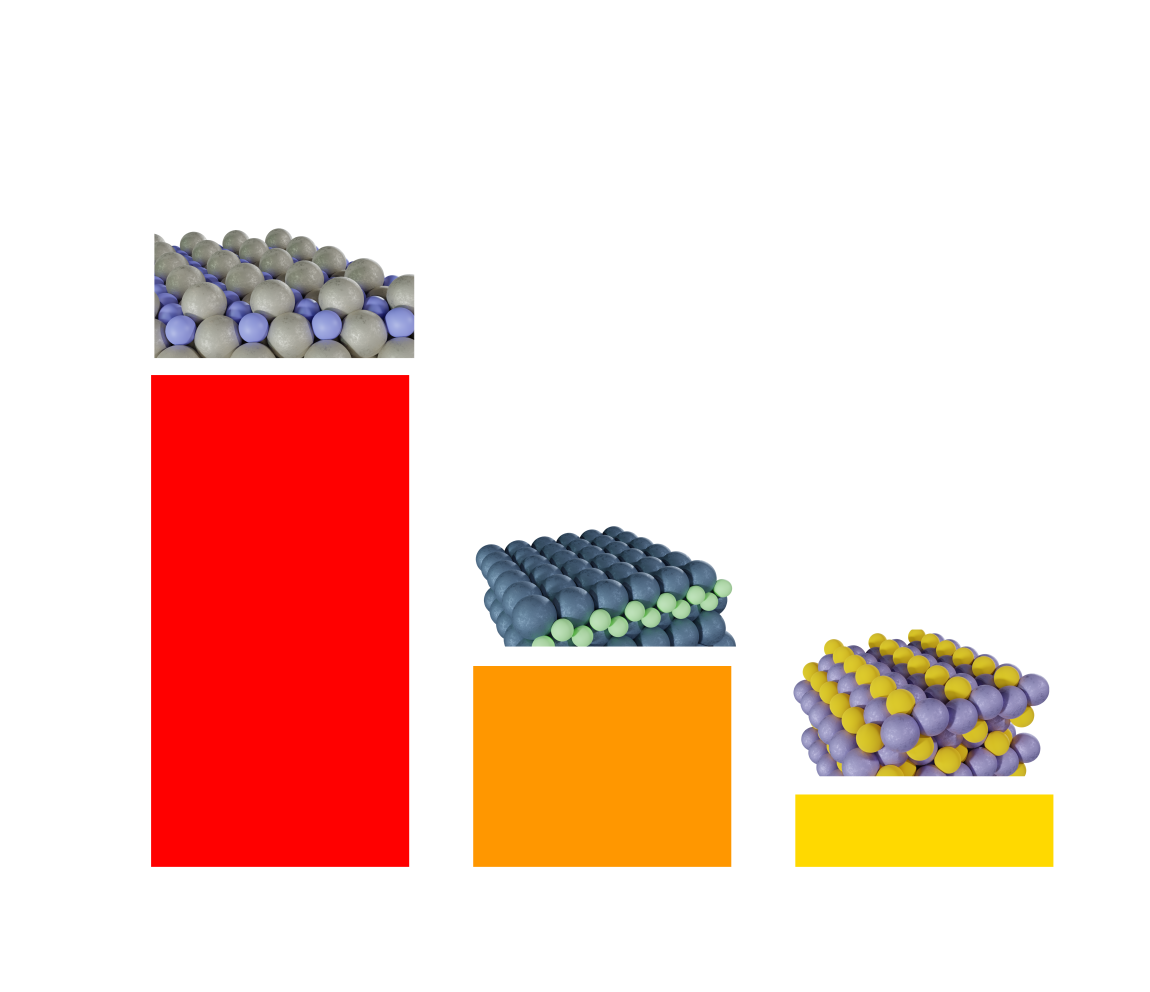
Select materials from the binary covalent alloy screening study. We found that the most active surfaces in our dataset tended
to have less occupied d-orbitals that were capable of strongly reducing the \( N_2 \) triple bond. However, all materials were
inevitably limited by the desorption of \( NH_3* \) from the surface.
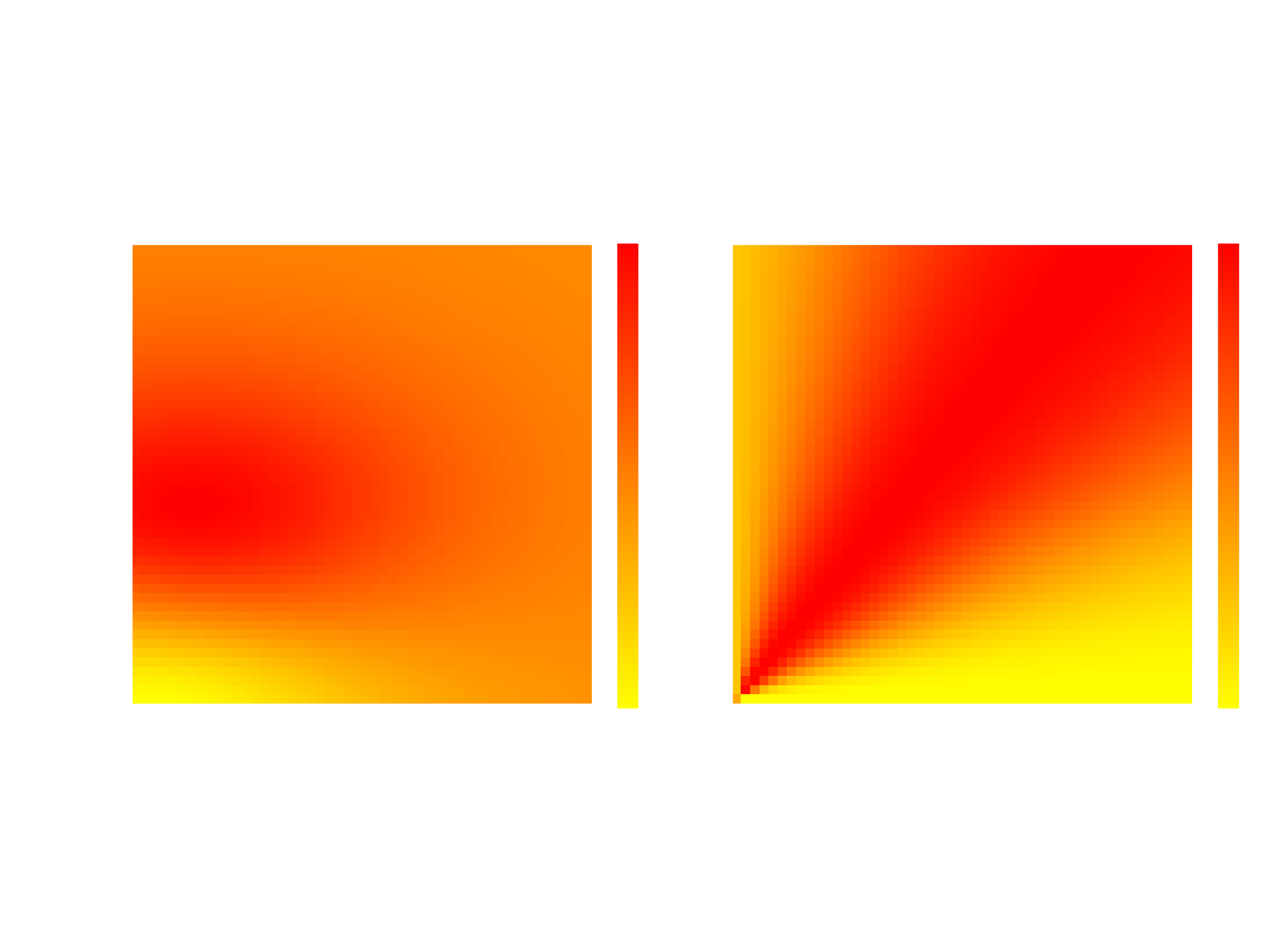
Bayesian Optimization model for battery electrolyte compositions. X and Y axes are fractions of chemicals
EC and NaPF6. The left panel shows the mean of the model and the right shows the
acquisiton function value, which is the
log expected improvement
.